How to decrypt a text using frequency analysis
I recently found a job offer in which, as a pre-selection process, wants to decrypt the following text and explain the procedure performed.
ΣΦΨΞΔλΨΔΛΣΦΔλΨξΔϗΞΔΦΨΞϑλΨΛΣΘϑΞϗΦϑλΨΣΞΨλϑΞΨζβΣφΔΨΣΦΨΣΞΨξΛϗ ΞΞϑΨϖΣΞΨΠΣϖΛΣφΔΞΨΩΨΠΛΣΦϖϗϖϑΨΔΨΞΔΨΘΔφϗΔΨϖΣΨΞϑλΨΓΔΘϗΦϑλΨΣΞΨ ΔΛΛϗΣΛϑΨαΔΨΣΞΨΔΛΛϗΣΛϑΨαΔΨΣλΨξΔΦϖΣΛΔΨϖΣΨΦϗΣξΞΔΨλβΨΠϑΦΓΡϑΨΔ ΞΨαϗΣΦμϑΨΞϑΨλΔΞβϖΔΦΨΞΔλΨεΞΔβμΔλΨϖΣΞΨΠΔζϑΦΔΞΨΩΨΔΦϗΘΔΦϖϑΨΞΔ ΨμΛϑΠΔΨΠΔΛΨΣλϑλΨΓΣΛΛϑλΨΣΞΨΔΛΛϗΣΛϑΨαΔΨΣΞΨΔΛΛϗΣΛϑΨαΔΨΞΔλΨΠΣ ΦΔλΨΩΨΞΔλΨαΔηβϗμΔλΨλΣΨαΔΦΨΠΔΛΨΞΔΨΘϗλΘΔΨλΣΦϖΔΨΞΔλΨΠΣΦΔλΨλϑ ΦΨϖΣΨΦϑλϑμΛϑλΨΞΔλΨαΔηβϗμΔλΨλϑΦΨΔζΣΦΔλ
I recently also read the book ‘The Code Book’ by Simon Singh, where he tells the whole history of cryptography and its uses, very good, and I highly recommend it.
So I thought it would be an interesting thing to do, I rolled up my sleeves and started.
Table of contents
Analysis of the situation and assumptions
At this point we know very little so let’s assume the following and see where it takes us
- That the original language of the message is in Spanish, since the job offer was in this language.
-
That one of the simplest and most historical encryptions was used, called classical cipher, more specifically a subset of it, called substitution cipher.
In a substitution cipher, letters (or groups of letters) are systematically replaced in the message by other letters (or groups of letters).
Frequency analysis
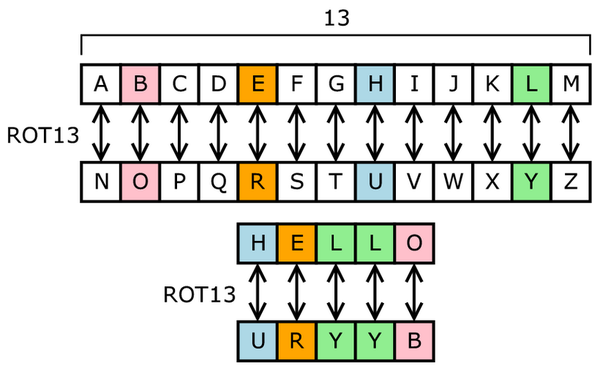
In order to break the encryption we are going to use the frequency analysis method.
Frequency analysis is based on the fact that, given a text, certain letters or combinations of letters appear more often than others, there are different frequencies for them.
For example:
- in Spanish the letter A and E are very common, while K and W are very rare
- in English the letter E, T and A are very common, while J, X and Z are very rare
Through a small program written in python we see the different signs used, and the amount of use of each one of them
from collections import Counter
text = "ΣΦΨΞΔλΨΔΛΣΦΔλΨξΔϗΞΔΦΨΞϑλΨΛΣΘϑΞϗΦϑλΨΣΞΨλϑΞΨζβΣφΔΨΣΦΨΣΞΨξΛϗΞΞϑΨϖΣΞΨΠΣϖΛΣφΔΞΨΩΨΠΛΣΦϖϗϖϑΨΔΨΞΔΨΘΔφϗΔΨϖΣΨΞϑλΨΓΔΘϗΦϑλΨΣΞΨΔΛΛϗΣΛϑΨαΔΨΣΞΨΔΛΛϗΣΛϑΨαΔΨΣλΨξΔΦϖΣΛΔΨϖΣΨΦϗΣξΞΔΨλβΨΠϑΦΓΡϑΨΔΞΨαϗΣΦμϑΨΞϑΨλΔΞβϖΔΦΨΞΔλΨεΞΔβμΔλΨϖΣΞΨΠΔζϑΦΔΞΨΩΨΔΦϗΘΔΦϖϑΨΞΔΨμΛϑΠΔΨΠΔΛΨΣλϑλΨΓΣΛΛϑλΨΣΞΨΔΛΛϗΣΛϑΨαΔΨΣΞΨΔΛΛϗΣΛϑΨαΔΨΞΔλΨΠΣΦΔλΨΩΨΞΔλΨαΔηβϗμΔλΨλΣΨαΔΦΨΠΔΛΨΞΔΨΘϗλΘΔΨλΣΦϖΔΨΞΔλΨΠΣΦΔλΨλϑΦΨϖΣΨΦϑλϑμΛϑλΨΞΔλΨαΔηβϗμΔλΨλϑΦΨΔζΣΦΔλ"
letters = Counter(text)
print("cantidad de letras = ", len(letters))
print(letters)
Obtaining the result:
Giving us some confirmation that we are doing well since 23 different signs are used, a value close to the amount of letters in the alphabet.
We also see that from highest to lowest in quantity of uses of a sign is: 74 - 53 - 34 - 31 - 31…
According to the following article (frequency of appearance of letters) in the Spanish language the letter ‘a’ is the most frequent, closely followed by the letter ‘e’, but exceeding them is the ‘space’ almost doubling the most frequent letter.
Then we replace the sign Ψ by a space, Δ by a ‘a’ and Σ by a ‘e’.
Note: Bear in mind of course that this is not an exact science, we are making use of probability. “It may fail” said Tusam. If this were the case you can go back and exchange the ‘a’ for the ‘e’ and continue the process.
We add the following lines of code to our program:
text = text.replace('Ψ', ' ')
text = text.replace('Δ', 'a')
text = text.replace('Σ', 'e')
print(text)
Obtaining:
Analyzing the result it is very possible that the sign ‘Ξ’ is an ‘l’, because in a word it is repeated 2 times in a row, and why would it be used for the words’ las’ ‘los’,’ el, ‘la’.
We make the replacement…
text = text.replace('Ξ', 'l')
Obtaining:
Continuing in the same way it is very possible that:
- Ω be a ‘y’
- ϑ be a ‘o’
- λ be a ‘s’
text = text.replace('Ω', 'y')
text = text.replace('ϑ', 'o')
text = text.replace('λ', 's')
Obtaining:
This is an iterative process, where in each iteration we get closer and closer to the goal.
From here it is much easier to deduce the rest, do you dare to complete it?
Good luck and see you!
